Что такое Египетский треугольник на стройке? В чем его особенность +Фото и Видео
Строительство с применением египетского треугольника древний способ, активно используемый до сих пор современными строителями. Название получил благодаря древнеегипетским сооружениям, хотя известно, что история его начинается задолго до этого периода.
Но, скорее всего, свойства уникальной фигуры не были оценены в те времена, пока не появился Пифагор, сумевший проанализировать и оценить изящные формы фигуры.
Египетский треугольник известен еще с древних времен. Он был и остается популярен в строительстве и архитектуре много веков.
Считается, что создал геометрическую конструкцию великий греческий математик Пифагор Самосский. Благодаря ему сегодня мы можем использовать все свойства геометрической постройки в области строения.
Египетский треугольник в строительстве. Общие сведения
Зарождение идеи
Идея у математика появилась после путешествия в Африку по просьбе Фалеса, который поставил задачу Пифагору изучить математику и астрономию тех мест. В Египте он среди бескрайней пустыни встретил величественные строения, поразившие его размером, изяществом и красотой.
Надо заметить, что более двух с половиной тысяч лет назад пирамиды были несколько другими – огромными, с четкими гранями. Тщательно изучив могущественные постройки, коих было не мало, так как рядом с великанами, стояли храмы поменьше, построенные для детей, жен и других родственных лиц фараона, это натолкнуло его на мысль.
Благодаря своим математическим способностям, Пифагор сумел определить закономерность в формах пирамиды, а умение анализировать и делать выводы привели к созданию одной из самых значимых теорий в истории геометрии.
Из истории
Знали ли в древнем Египте о геометрии и математике? Конечно да. Жизнь египтян была тесно связана с наукой. Они регулярно пользовались знаниями при разметке полей, создании архитектурных шедевров. Даже существовала своя служба землемеров, которые применяли геометрические правила, занимаясь восстановлением границ.
Название треугольник получил благодаря эллинам, которые нередко бывали в Египте в VII-V вв. до н.э. Считается, что прообразом фигуры стала пирамида Хеопса, отличающаяся совершенными пропорциями. Ее место особенное в истории. Если посмотреть поперечное сечение, то можно отметить два треугольника, у которых угол внутри равняется 51 о 50’.
Строение
Сегодня это строение усеченной формы, приобретенной под воздействием времени, высота явно потерялась. Однако, восстановив ее геометричность, можно сделать вывод, что стороны треугольников равны. Получается в основе заложен золотой прямоугольный треугольник.
Однако, следует рассмотреть другую пирамиду – Хефрена, у которой основа как раз-таки прямоугольный треугольник и где угол наклона боковых граней равен 53 о 12 с соотношением катетов 4:3. Это уже так называемый священный треугольник. Для египтян такая фигура сопоставлялась с семейным очагом: катет вертикального положения олицетворял мужчину, основание – представительницу прекрасного пола, а гипотенуза – рождение ребенка от обоих.
Стороны пирамиды Хефрена в соотношении равны 3:4:5, что точно соответствует теореме Пифагора. Значит, можно сделать вывод, что строители уже знали об этой теореме, но не могли ее сформулировать. Хотя, в исторических письменах встречаются следы использования египетского треугольника за много веков даже до Египта. До сегодняшнего дня это загадка, как могли такие знания получить древние египтяне. Понимали ли они чем обладают?
Особенность фигуры к тому же в том, что благодаря подобному соотношению, она является простым и первым Героновым треугольником, так как ее стороны и площадь целочисленные.
Обратное доказательство
Как доказать, что треугольник прямоугольный? Нужно порой исходить от обратного, то есть если сумма квадратов обеих сторон равна квадрату третьей, то треугольник прямоугольный, что подтверждает равенство 3 2 х4 2 =5 2 и значит он действительно прямоугольный.
Таким образом теорема Пифагора стала каноном и фундаментом развития математической науки. Со школьной скамьи каждый ученик знает, что означает выражение «Пифагоровы штаны во все стороны равны».
Интересно, что теорема Пифагора находится в Книге Гиннесса как теорема, обладающая самым большим количеством доказательств, которых примерно 500.
Особенности
Если рассмотреть более детально отличительные особенности египетского треугольника, то можно выделить следующие моменты:
- все стороны и площадь состоят из целых чисел, как говорилось выше;
- согласно теории великого математика, сумма квадратов катетов равна квадрату гипотенузе;
- такой фигурой возможно отмерить прямые углы в пространстве. Это используется в процессе строительства до сих пор;
- не обязательно пользоваться специальными измерительными приборами, подойдут подручные средства, например, веревка.
Место в строительном мире
С древнейших времен египетский треугольник нашел почетное место в архитектуре и строительстве. Конструкция пирамиды отличается тем, что позволяет создавать здание с совершенно правильными углами без каких-либо дополнительных инструментов.
Задача намного облегчается, если использовать транспортир или треугольник. Но, раньше применялись только шнуры и веревке, разделенные на отрезки. Благодаря отметкам на веревке можно было с точностью воссоздать прямоугольную фигуру. Строителям заменяла транспортир и угольник веревка, для чего отмечали узлами на ней 12 частей и складывали треугольник с отрезками 3,4,5. Прямой угол получался без затруднений. Эти знания помогли создать множество сооружений, в том числе пирамиды.
Интересно, что до древнего Египта, таким способом строили в Китае, Вавилоне, Месопотамии.
Свойства египетской треугольной фигуры подчиняются истине – квадрат гипотенузы равен квадратам двух катетов. Эта теорема Пифагора знакома каждому со школьной поры. Например, умножаем 5х5 и получаем гипотенузу равную числу 25. Квадраты обоих катетов равны 16 и 9, что в сумме дает цифру 25.
Благодаря таким свойствам, треугольник нашел применение в строительстве. Можно взять любую деталь, с целью провести линию прямого направления с условием, что ее длина должна быть кратной пяти. После этого заметить один край и прочертить от него линию кратную четырем, а от другого кратную трем. При этом каждый отрезок должен быть длиной минимум четыре и три. Пересекаясь, они образовывают один прямой угол в 90 градусов. Другие углы равны 53,13 и 36,87 градусам.
Какие существуют альтернативные варианты
Как создать прямой угол
Лучшим вариантом смастерить прямой угол является применение угольника или транспортира. Это позволит с минимальными затратами найти необходимые пропорции. Но, основной момент египетского треугольника в его универсальности из-за возможности создать фигуру, не имея под рукой ничего.
В этом деле может пригодиться все, даже печатные издания. Любая книга или даже журнал имеют всегда соотношение сторон, образующее прямой угол. Типографские станки работают всегда точно, чтобы рулон, заправленный в машину резался пропорциональными углами.
Древние инженеры придумывали много способов строительства египетского треугольника и всегда экономили ресурсы.
Поэтому, самым простым и широко применяемым был метод постройки геометрической фигуры с применением обычной веревки. Бралась бечевка и резалась на 12 ровных частей, из которых выкладывалась фигура с пропорциями 3,4 и 5.
Как создать другие углы?
Египетский треугольник в строительном мире нельзя недооценивать. Его свойства однозначно полезны, но без возможности построить углы другого градуса в строительстве невозможно. Чтобы образовался угол в 45 градусов, понадобится рамка или багет, которые распиливаются под углом в 45 градусов и соединяются между собой.
Важно! Чтобы получить необходимый наклон, потребуется позаимствовать бумажный лист из печатного издания и согнуть его. Линии изгиба при этом будут проходить через угол. Края должны быть соединены.
Получить 60 градусов можно с применением двух треугольников по 30 градусов. Чаще всего используются для создания декоративных элементов.
Небольшие хитрости
Египетский треугольник 3х4х5 актуален для маленьких домов. Но, что делать, если дом 12х15?
Для этого нужно построить прямоугольный треугольник, у которого катеты равняются 12 и 15 м. Гипотенуза находится как квадратный корень из суммы 12х12 и 15х15. В итоге получаем 19,2 м. С помощью чего-либо — веревки, шпагата, бечевки, тросика, военного кабеля, отмеряем 12, 15 и 19,2 м. Делаем узлы на этих местах и ставим жимки.
Затем треугольник нужно растянуть на нужном месте и установить 3 точки опоры, в которые вбить колышки. Четвертую точку можно получить, не трогая концы катетов. Для этого точка прямого угла перекидывается по диагонали и все готово.
Например, есть участок, где требуется прямой угол – для места под кухонный гарнитур, раскладки кафеля и других моментов. Хорошо бы такие вопросы учесть при кладке, но реальность другая и не всегда попадаются ровные стены и прямые углы. Здесь пригодится египетский треугольник с соотношением 3:4:5, либо при необходимости 1,5:2:2,5.
Обязательно учитывается толщина маяков, погрешность, бугры на стенах и т.д. Треугольник рисуется с помощью рулетки и мела. Если разметка небольшая, то можно воспользоваться листом гипсокартона, так как режутся они с правильными углами.
Египетский треугольник широко использовался в строительстве целых 2,5 века. И сегодня иногда приходится применять данную методику, при отсутствии необходимых инструментов, чтобы получить прямые углы. Свойства этой фигуры уникальны, что гарантирует точность в архитектуре и строительстве, без которой не обойтись. С ним легко работать, по форме он гармоничен и красив. До сих пор пытливые умы пытаются разгадать тайну египетского треугольника.
Разметка под фундамент своими руками
Качество постройки в огромной степени зависит от того, насколько правильно была выполнена разметка под фундамент. Занимаясь этой работой важно с максимальной точностью выдержать все прямые углы. Разметка фундамента своими руками под частный дом может быть выполнена несколькими способами. Чаще всего используются метод «египетского» треугольника и метод двух кривых. Поэтому в этой статье рассмотрим именно их.
Какие инструменты понадобятся?
Производится разметка фундамента своими руками с применением инструментов:
- Рулетки;
- Шнура;
- Гидроуровня и отвеса;
- Помимо этого понадобятся деревянные колышки.
С чего начать разметку?
Итак, как провести разметку фундамента? Для начала следует определить две исходные точки, вбив колышки по углам будущего здания, находящимся на одной прямой со стороны его самой длинной стены. Далее от них нужно будет провести перпендикуляры, таким образом отметив внешний контур смежных стен.
«Египетский треугольник». Самый простой метод
Разметка фундамента своими руками быстрее всего может быть произведена методом «золотого» треугольника, имеющего соотношение длин сторон 5*3*4. Мероприятие при этом выполняется в несколько этапов:
1. Для начала нужно найти длинную веревку и завязать на ней четыре узла. Первый – на конце, второй на расстоянии 3м, третий в четырех метрах от второго и последний в пяти метрах от третьего;
2. После этого самый первый и самый последний узлы соединяют гвоздем. По гвоздю следует вбить и в каждый из промежуточных узлов;
3. При этом длинную сторону получившегося треугольника нужно расположить вдоль линии между двумя уже вбитыми колышками;
4. Вдоль короткой стороны проводят требуемый перпендикуляр;
5. На полученной прямой, вбивают третий колышек на расстоянии равном ширине здания.
Важно: Правильность всех замеров следует обязательно проверить. Для этого между вбитыми кольями по диагоналям натягивают два шнура и связывают в месте пересечения.
Paste a VALID AdSense code in Ads Elite Plugin options before activating it.
Метод двух дуг
Разметка фундамента своими силами этим методом выполняется также с использованием веревки. Предварительно от одного из колышков в обе стороны по уже имеющейся прямой отмеряют равные расстояния и отмечают найденные места. Далее к одной из полученных точек прикрепляют веревку с привязанным на противоположном конце гвоздем. Натянув ее проводят дугу напротив того колышка, от которого отмерялись расстояния. Затем веревку крепят ко второму отмеченному месту и чертят еще одну дугу. Из той точки, где дуги пересекутся, проводят линию к колышку. В результате получается прямой угол между ней и уже имеющейся линией.
На заключительном этапе к кольям на высоте будущего фундамента привязывают шнур, поверяя горизонтальность его положения со всех четырех сторон, пользуясь строительным уровнем. Для ленточного фундамента чертят внутренний контур параллельно найденному внешнему и также натягивают шнур.
Совет: В том случае, если траншею предполагается копать с привлечением техники, шнуры лучше не использовать. В процессе работы они могут порваться. Линии между найденными точками в этом случае стоит прочертить песком. Для нахождения центров столбов столбчатого фундамента, от найденных углов вдоль прочерченных линий отмеряют необходимые расстояния и ставят отметки. Далее проверяют прямоугольность углов, получившихся на пересечении линий (соединяющей полученные точки на противоположных сторонах и линии периметра, на которой расположены отметки).
Разметка фундамента своими руками, как можно было заметить – процедура не такая уж и сложная. Самое главное, делать все аккуратно, хорошо натягивать веревку и обязательно проверять полученный результат методом диагоналей.
Египетский треугольник, его свойства
О египетском треугольнике и его свойствах хорошо известно ещё с древних времён. Эта фигура широко применялась в строительстве для разметки и построения правильных углов.
История египетского треугольника
Создателем этой геометрической конструкции является один из величайших математиков древности Пифагор. Именно благодаря его математическим изысканиям мы можем в полной мере использовать все свойства данного геометрического построения в строительстве.
Можно предположить, что математические навыки позволили Пифагору заметить закономерность в формах строения. Дальнейшее развитие событий можно легко представить. Базовый анализ и построение выводов создали одну из самых значимых фигур в истории. Скорее всего, в качестве прообраза была выбрана именно пирамида Хеопса из-за своих практически совершенных пропорций.
Египетский треугольник в строительстве
Свойства этой уникальной геометрической конструкции заключаются в том, что её построение без применения каких-либо инструментов позволяет построить дом с правильными во всех соотношениях углами.
Итак, качества египетского треугольника позволяют делать правильные во всех соотношениях углы. Стороны конструкции имеют следующее соотношение друг к другу:
Чтобы проверить ту ли фигуру вы начертили, используйте хорошо известную ещё со школьной скамьи Теорему Пифагора.
Для лучшего понимания возьмём приведенную выше зависимость и составим небольшой пример. Умножим пять на пять. В результате чего получим гипотенузу равную 25. Вычислим квадраты двух катетов. Они составят 16 и 9. Соответственно их сумма будет двадцать пять.
Именно поэтому свойства египетского треугольника так часто используются в строительстве. Вам достаточно взять заготовку и прочертить прямую линию. Её длина всегда должна быть кратной 5. Затем нужно наметить один край и отмерять от него линию кратную 4, а от второго 3.
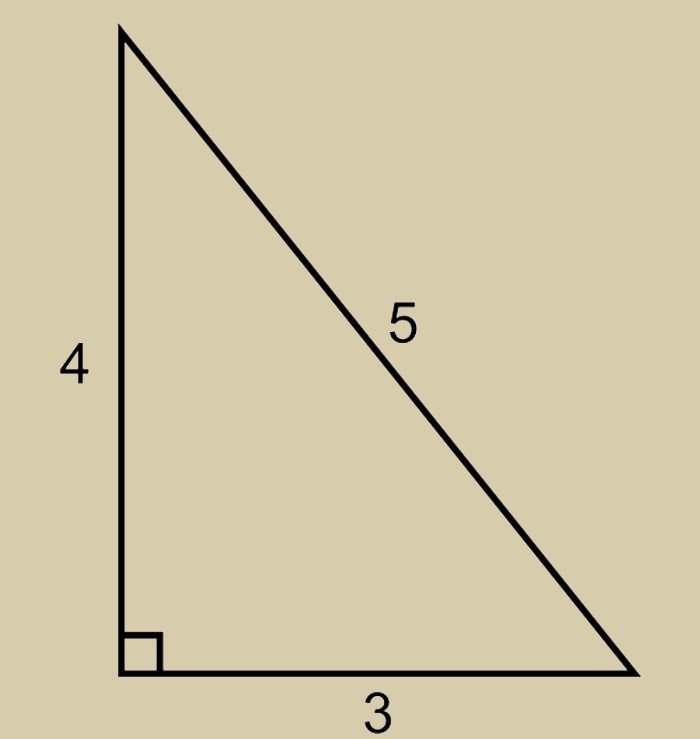
Альтернативные способы построить прямой угол на 90 градусов
Как уже упоминалось выше, наилучшим вариантом будет просто взять угольник или транспортир. Эти инструменты позволяют с наименьшими затратами времени и сил добиться нужных пропорций. Главное же свойство египетского треугольника заключается в его универсальности. Фигуру можно построить, не имея в арсенале практически ничего.
Сильно в построении прямого угла помогают простые печатные издания. Возьмите любой журнал или книгу. Дело в том, что в них соотношение сторон всегда составляет ровно 90 градусов. Типографические станки работают очень точно. В противном случае рулон, который заправляется в станок, будет резаться непропорциональными кривыми углами.
Как получить египетский треугольник при помощи верёвки
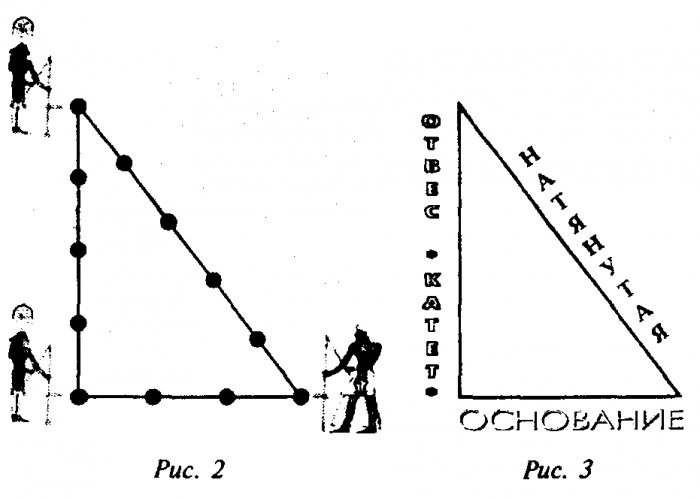
Свойства этой геометрической фигуры тяжело переоценить. Неудивительно, что инженерами древности было придумано множество способов её образования с использованием минимальных ресурсов.
Одним из самых простых считается метод образования египетского треугольника со всеми его вытекающими свойствами посредством простой верёвки. Возьмите бечёвку и разрежьте её на 12 абсолютно ровных частей. Из них сложите фигуру с пропорциями 3, 4 и 5.
Как построить угол в 45, 30 и 60 градусов
Безусловно, египетский треугольник и его свойства очень полезны при постройке дома. Но без других углов вам обойтись всё-таки не удастся. Чтобы получить угол, равняющийся 45 градусам, возьмите материал рамки или багета. После чего распилите его под углом в сорок пять градусов и состыкуйте половинки друг с другом.
Как видите, свойства фигуры позволяют гораздо проще и быстрее построить геометрический конструкт. Чтобы добиться соотношения сторон в 60 градусов нужно взять один треугольник на 30º и второй такой же. Обычно подобные пропорции необходимы при создании определённых декоративных элементов.
Итоги
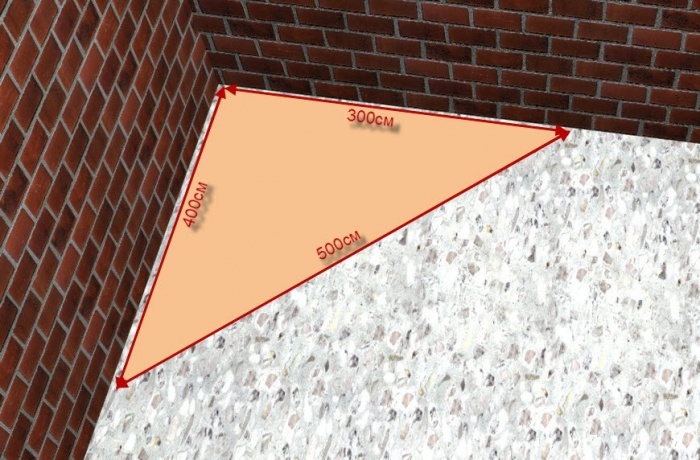
Свойства египетского треугольника широко использовались в строительстве на протяжении почти, что двух с половиной веков. Даже сейчас при недостатке инструментов строители применяют эту открытую ещё Пифагором методику, чтобы добиться ровных прямых углов.
Портал о стройке
На чертеже проведем отрезок прямой линии любой длины и разделим его пополам. Но для большей наглядности воспользуемся теми же цифровыми выражениями, которые имеются в египетском треугольнике: 3, 4, 5. В качестве исходного отрезка (рис. 1) изобразим отрезок АВ, длину которого примем равным 3 + 5 = 8, и посмотрим, в каком соотношении он будет разделен геометрическими построениями. Для начала разделим отрезок АВ пополам: АД = ДВ = 4. Теперь из конца В отрезка АВ восстановим перпендикуляр ОВ, равный половине длины АВ. То есть ОВ = АД = ДВ = 4. Затем из точки О проведем окружность радиусом ОВ и соединим точки А и О прямой линией. Пересечение этой линии с окружностью обозначим точкой С, после чего проведем через нее дугу окружности, радиус которой равен АС. Дуга разделит отрезок АВ на две неравные части, которые находятся в соотношении АК : ВК = 1,618. Все в полном соответствии с золотым сечением. Задача решена? Да, отрезок разделен в нужном соотношении.
Но у задачи есть продолжение, имеющее самое непосредственное отношение к египетскому треугольнику и некоторым тайнам пирамид.
Рис.1. При делении отрезка АВ = 8 в крайнем и среднем отношении искомая точка K делит отрезок АВ на две части: АК = 4.944 и ВК = 3.056. При этом АВ:АК=8:4.944 = 1.618 и АК:ВК = 4.944:3,056 = 1,618. Полученное таким образам число 1.618 называлось золотым, а сам процесс деления отрезка а крайнем и среднем отношении — золотым сечением.
В Древнем Египте применяли другой, очень близкий к золотому сечению метод деления отрезка АВ = 8. Искомая точка Е делила отрезок АВ на две части в отношении 5:3. В данном случае АЕ = 5 и ВЕ = 3. При этом АВ:АЕ = 8:5 = 1,6 и АЕ:ВЕ = 5:3 = 1,666. Этот метод позволял выразить закономерности золотого сечения с помощью целых чисел «египетского» прямоугольного треугольника ОВЕ с соотношением сторон 3:4:5. Он был очень удобным для практического применения и являлся в Египте своеобразным стандартом. Образующиеся при таком делении отрезка соотношения ОВ: АВ — 1:2. ОВ:ЕФ = 2:3, ВЕ:ОВ:ОЕ: — 3:4:5, а также углы 26°34′ и 53°08′ закладывались при проектных, разметочных и строительных работах в конструкции пирамид и других сооружений. Равнобедренный треугольник ОЕФ являлся сечением пирамиды, проведенным через середины двух противоположных граней. Такая пирамида удовлетворяла требованиям «египетского» треугольника, а практически — золотому сечению с допустимой точностью. Угол 26°34′, равный половине угла 53°08′. использовался в основном при строительстве наклонных галерей, лестниц, коридоров… Такой наклон имеет, например, коридор пирамиды Хеопса (рис. 2).
Если соединить точки О и Е прямой, то получим прямоугольный египетский треугольник ЕОВ с соотношением сторон ВЕ : ВО : ЕО = 3:4:5. Ну кто бы мог подумать, что он прячется в таком месте! Что он незримо присутствует при делении отрезка в среднем и крайнем отношениях! Что он дитя золотого сечения и как бы находится с ним в родственной связи! Одним словом, там. где египетский треугольник — ищите золотое сечение. И наоборот: заметив золотое сечение, ищите поблизости и египетский треугольник.
Ранее на сайте: «Мост ослов» и священные числа 3, 4, 5, 12
В треугольнике ЕОВ угол ОЕВ равен 53°08′. Его легко вычислить через тангенс: ОВ : ЕВ = 4 : 3 = 1,333. Угол 53°08′ имеет самое прямое отношение к пирамидам Хеопса. Хефрена, Микерина. Да и к большинству других пирамид Египта. Например, у пирамиды Хефрена угол наклона грани к основанию практически равен углу египетского треугольника. Угол наклона боковых граней пирамид Хеопса и Микерина близок к теоретическому. Разница всего в один-два градуса. Выходит, что пирамиды строились с расчетом как можно точнее выполнить условия золотого сечения. Не удивительно, что пирамиды в Гизе до сих пор не разрушились.
Рис.2. В пирамиде Хеопса (справа) углы наклона граней и входного коридора близки к углам треугольников, образованных при делении отрезка в среднем и крайнем отношении (рис. 1). А в пирамиде Хефрена (слева) угол наклона граней практически равен углу 53°08′. Погрешность всего четыре минуты’
Геометрическое построение, показанное на рис. 1, скрывает еще один секрет, имеющий отношение к пирамидам. «Спрятан» он в прямоугольном треугольнике АОВ. Вернее, в величине угла ОАВ. Его можно вычислить с помощью тангенса: ОВ : АВ = 4:8 = 0,5. Тангенсу 0.5 соответствует угол 26°34′. И здесь выясняется, что он равен половине угла ОЕВ: 53°08′: 2 = 26°34′. Если теперь сравнить величину этого угла с углом наклона коридора, ведущего внутрь пирамиды Хеопса, мы не увидим существенной разницы! (рис. 2). Посмотрим еще раз на этот треугольник АОВ с несколько другой стороны. В нем ОВ : АВ = 4:8 = 1:2. Опять соотношение из золотого ряда! Так, при делении отрезка в среднем и крайнем отношении, мы получили целый ряд чисел, связанных прямо или косвенно с золотым сечением: 1,618; 1:2, 2:3, 3:4:5. Вот тебе и египетский треугольник! Оказывается, что он лишь главное звено в длинной цепи взаимосвязанных знаний, взявшись за которое можно последовательно вытащить все остальные. Недаром, видно, нам пришлось провести столько времени на «мосту ослов», чтобы с помощью египетского треугольника понять целую философию мироздания, угадать принципы, легшие в основу создания природы. Но об этом — в других главах.
Египетский треугольник
Автор: admin · Апрель 8, 2014
Египетский треугольник.
Название «египетский треугольник» появилось уже в 5 веке до н.э. Принадлежит оно прямоугольному треугольнику, стороны которого равны соответственно 3, 4 и 5.
Назван он был так потому, что очень широко применялся еще в Древнем Египте в различных сферах жизнедеятельности.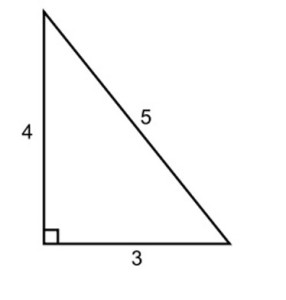
Хотя уже тогда он был знаком людям далеко за пределами Древнего Египта, но, видимо, его уникальные свойства заметили и начали использовать впервые именно там.
В чем же состоит его отличительная особенность?
Во-первых, все его стороны и площадь — это целые числа;
во-вторых, сумма квадратов катетов равна квадрату гипотенузе ( а это ведь теорема Пифагора, которую все знают со школы! Но о Пифагоре чуть позже);
в-третьих, это то, что с его помощью можно отмерять прямые углы в пространстве (треугольник-то прямоугольный!), а это просто необходимо, например, в строительстве;
и, в-четвертых, этот треугольник можно запросто построить с помощью простой веревки.
В пространстве достаточно сложно отложить прямой угол, (как же это сделать, когда в природе редко встретишь прямые линии, а уж тем более прямые углы, не от чего отталкиваться!), но египтяне изобрели интересный способ. Они брали веревку, отмеряли на ней узелками 12 частей, а потом складывали из нее треугольник, стороны которого равны 3 , 4 и 5 частям соответственно. В этом треугольнике прямой угол получался сам собой! А уже имея такой инструмент, они могли с большой точностью строить свои сооружения, например, пирамиды. А также использовать его для разметки земли под сельскохозяйственные работы.
А теперь про Пифагора. Египетский треугольник тесно связан с его именем.
Возможно, изучение интересных особенностей египетского треугольника и подтолкнуло Пифагора на попытку обобщения зависимостей во всех других прямоугольных треугольниках. Что ему, как известно, удалось!
Кстати, оказывается, теорема Пифагора попала в Книгу Рекордов Гиннеса как теорема с самым большим количеством доказательств (их насчитывается около 500).
Египетский треугольник – доклад сообщение
Со времен античности до настоящего времени в разных сферах жизнедеятельности человека существует огромное количество бесценных открытий.
Среди них почетное место занимает всемирно известный “Египетский” треугольник. вавилонская геометрия славилась тем, что в ее пределах велась работам прямоугольным треугольником с сочетанием 3:4:5.
История его появления связана с наблюдениями эллинов за основой пирамиды Хеопса в Египетском государстве еще в v веке до г. э. По одной из версий название этому треугольнику было дано древними греками. Второе ее название – “Золотой треугольник”.
Среди этих людей был ученый Пифагор Саросский, который особое внимание обратил на формы этой великой постройки. Так повелось, что с древних пор именно этот треугольник архитекторы применяли для достижения определенных пропорций строения. Теорема Пифагора, которая стала открытием, используется в настоящее время. Ученый изначально делал попытку обобщения отношения квадратов, характерных для египетского треугольника.
В строительстве правило его использования незаменимо. Это связано с тем, что при определенном произведении линий образуется угол в 90, 53 градусов 13 минут и 36 градусов 86 минут. Именно такие параметры имеет всемирно известная пирамида Хефена.
Особенностями египетского треугольника является его площадь и стороны – целые числа, также при использовании обычной веревки можно изобразить этот треугольник без труда. К этому способу обращались зачастую землемеры, которые с ее помощью выводили прямой угол.
В настоящее время также рабочие, связанные со стройкой, нередко обращаются к этой методике, чтобы при необходимости получить ровные прямые углы. Это было связано с тем, что в далеком прошлом было недостаточно инструментов для качественного процесса строительства зданий.
Таким образом, “Египетский треугольник” – это уникальная геометрическая конструкция, известная с давних пор. Прообразом этой фигуры является одна из египетских пирамид, на которую обратил внимание во время своего путешествия математик древности – Пифагор.
Ее особенность состоит в том, что, например, обычная идея построить дом возможна без обращения к угольнику или транспортиру. Грамотный подход и знания строителя, правильное соотношение всех углов возможно при грамотном подходе с построением этого треугольника.
Картинка к сообщению Египетский треугольник
Популярные сегодня сообщения и доклады
Бурундук принадлежит к семейству беличьих. Всего существует около двадцати пяти видов бурундуков. Большее количество видов обитает в Северной Америке.
Исследование космоса интересовало человечество на протяжении многих сотен лет. Освоение космоса – опасный труд, на который способен не каждый. Великими героями космоса можно назвать немногих.
Период обучения в Царскосельском лицее представляет собой основу для развития поэтического дарования Пушкина под влиянием не только талантливых педагогов, но и одаренных, умных и верный друзе
Лес – это дом для многих животных и птиц. Ниже расскажу о некоторых из них. 1. Лось – самый большой из обитающих в наши дни оленей. После бизона, это второе по размеру
Не самое большое государство, которое произошло от Казахского ханства и находится в середине Евразии, поэтому Казахстан разделяется на европейскую и азиатскую часть по расположению на материк
ражданин этот термин обозначает человека, который проживает на территории государства (вместе с другим населением), он по праву пользуется правами (защита, права) которое предоставляет ему го
Что такое Египетский треугольник на стройке
Египетский треугольник — – прямоугольный треугольник с соотношением сторон 3:4:5. Сумма указанных чисел (3+4+5=12) с древних времен использовалась как единица кратности при построении прямых углов с помощью веревки, размеченной узлами на 3/12 и 7/12 ее длины. Применялся… … Словарь строителя
Египетский треугольник — прямоугольный треугольник с отношением сторон 3:4:5 (сумма чисел 3 + 4 + 5 = 12). Землемеры и архитекторы с глубокой древности пользовались соотношением этих чисел для построения прямых углов с помощью верёвки, размеченной узлами на 3/12 и… … Архитектурный словарь
Египетский Треугольник — Прямоугольный треугольник с соотношением сторон 3:4:5. Сумма указанных чисел (3+4+5=12) с древних времен использовалась как единица кратности при построении прямых углов с помощью веревки, размеченной узлами на 3/12 и 7/12 ее длины. Применялся в… … Строительный словарь
лунный египетский треугольник — Треугольник, возникающий в центре большого квадрата, построенного на базе трёх лунных обелисков с отношением сторон 3:4:5, при условии, что вся площадь квадрата разделена на серию прямоугольных треугольников с отношением катетов 1:2. E. Egyptian… … Толковый уфологический словарь с эквивалентами на английском и немецком языках
Треугольник (значения) — В Викисловаре есть статья «треугольник» Треугольник в широком смысле объект треугольной формы, либо тройка объектов, попарно связ … Википедия
Треугольник Халаиба — Халаибский треугольник مثلث حلايب спорная территория ← … Википедия
Египетский крест (астеризм) — В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете … Википедия
Египетский лук — Угловой лук у стрелка на колеснице и простой у пехотинца Египетские луки, как стрелковое оружие прошли определенный путь эволюционного развития от простого из одного вида дерева до сложносоставного («углового») из разных видов… … Википедия
Халаибский треугольник — مثلث حلايب спорная территория ← … Википедия
Зимний треугольник — красный цвет = зимний треугольник, синий цвет = зимний круг … Википедия
Источники:
http://postroju-dom.ru/fundament/10-razmetka-pod-fundament-svoimi-rukami
http://bouw.ru/term/egipetskiy-treugolynik
http://stroyka.ahuman.ru/kak-postroit-egipetskij-treugolnik/
http://lubopitnie.ru/egipetskiy-treugolnik/
http://doklad-i-referat.ru/soobshchenie/matematika/egipetskij-treugolnik
http://dic.academic.ru/dic.nsf/ruwiki/27305
http://pos-art.ru/poleznye-sovety/jepoksidnaja-smola-proporcija-s-otverditelem.html
Загрузка...